Let’s take the following board as an example:
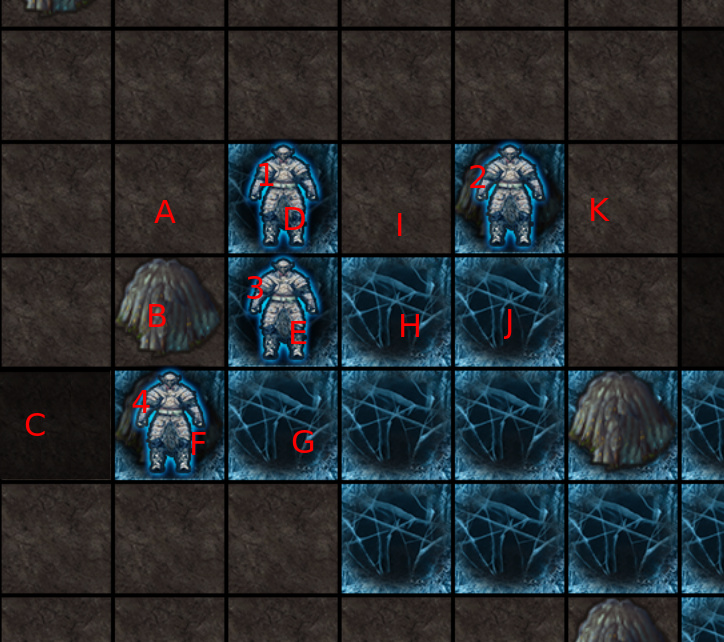
We see some units (1-4) and cells (A-K).
Both unit 3 and 4 would like to move to cell B. So we could send unit 3 there and let unit 4 wait.
The alternative is to make unit 4 take cell B and 3 waiting or going up to D. Let’s assume that D is the closest to the opponent, so moving unit 3 upwards and letting 4 take the empty cell would be the best.
So we assign a score for each unit in combination with each cell:

Empty cells are 0, left out for readability.
As the Hungarian method requires a square matrix, we have to add additional rows (units) to it.
These are just 0s everywhere (no score for doing anything).
Then we can just feed it into our algorithm, that we copied from github 
This requires O(n^3) time and gives us one optimal assignment for units to cells.
Note: most implementations use a cost matrix rather than score, so we have to multiply every value by -1.
In my example I used the same score for any unit occupying a cell. You can vary the function, e.g. prioritizing high level units at the front over low level ones or not giving a reward for a lvl3 unit entering a neutral cell.
Edit: the forum was lagging, I didn’t even see that @_CG_SaiksyApo replied before me 