A* Craft - Feedback & Strategies

Contests
#30

Finished 2nd, 10988 points.

I used simulated annealing as well, but instead of working directly on arrows, I worked on a set of cycles (starting with an empty set).

For example, let say that I have a set of cycles like this:

1

For the evaluation I simulate the robots, and when one enters a cycle, it follows it, (while putting arrows if it was not already done by a previous robot).
The way to go through the cycle depends only on the first robot entering it.
So after a simulation I might have something like this:

2

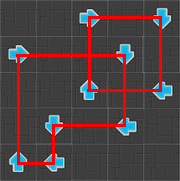
For the simulated annealing, in order to go from one state to another I add another small cycle to it this set of cycles.
If an edge is present twice, it is removed (so itā€™s more a ā€˜xorā€™ with another cycle, than an addition).

If we add this small cycle to the previous state:

3

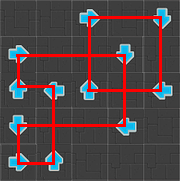
Weā€™ve got this:

4

Which might give something like that after a simulation:

5

The small cycles I used were these ones (and the rotations):

6

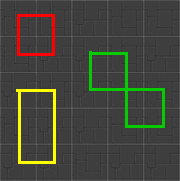
Sometimes adding a small cycle like this can split/merge cycles, sometimes it can reverse a part of a cycle, etc.

One other thing is that the cycles are not necessary on free cells only, they can partially be over void cells, or fixed arrows cells, so it can work (kind of) on test cases without big open area too.

The good thing with this approach, is that it creates a ā€œsmoothā€ search space : it can go from one good state to another without going too low with the evaluation function, and for simulated annealing this is often critical, and I think it has some good scores on tests with big open area.

The bad thing is that it requires some hacks to handle the robots before they enter the cycles, or when you want them to do a 180, and because of that it behave badly on some cases (I almost always miss the 354 points solution of the test #13 by more than 150 points, I should have brute-forced this kind of test cases :roll_eyes:).

27 Likes
#31

Damn I wish we have a multiplayer version soon.

I canā€™t stand waiting to see how my algorithm perform once I finished debugging it. As I started implementing too late and couldnā€™t finish in time, I lacked one or two hours probablyā€¦

#32

That was a good contest.
Iā€™m 359th with a very simple IA placing a random arrow on each dead-end and computing score, keeping the best combination of arrows.
Several improvements to test when it will be a multiplayers game.

#33

The map has two axial symmetries and a point symmetry. Which allows you to search on only one quarter of the map.

The two axial symmetries are equivalent to a point symmetry, except on the vertical symmetry line where you cannot place left/right arrows without breaking either the horizontal axial symmetry (e.g: pair of black arrows) or the central symmetry (e.g: pair of yellow arrows).
Two_Axes_And_Point_Symmetry

Edit: @eulerscheZahl gave a counter-example in PM. If your solution respects an axial symmetry there is seemingly no way of going from one side of the map to the other without dying very quickly, which is probably not the optimal solution ( ā†’ā€¦|ā€¦ā†). As for point symmetry it also seems like a very bad idea as you will just make 1 circle and die.

#34

Finished #76 (7883 points)

Very nice contest for this duration.

Initially I did random search robot by robot (computing full path for one robot then then create a path for remaining robots) This took me to 3600 points.The score I calculated during random search was differing from actual score. Once I fixed those bugs, I reached 4200 points. Then I converted my random search in such a way that I choose a random move for all robots together in each step. This took me to 4800ish. When I was out of ideas MadKnight suggested me to try mutation. So I tried my first mutation and crossover in this contest. Once I implemented my first add arrows mutation my score jumped to 6000+. Then I added delete arrows and change arrow direction. (As someone suggested I also tried moving arrow to one position. But this didnā€™t help me) By this time my score was 7000+

Crossover was a failure strategy for this contest.
Attempt 1) Find a random solution with only 1 robot (for all robots). Mutate each of these solution to improve the global score. Run a crossover in all these solutions. Mutate this solution for several iterations.

Attempt 2) Take the two best random solutions. Mutate them separately. Apply crossover on these two mutated solutions. Then mutate this solution for several iterations.

Attempt 3) Same as attempt 2 but I pick n best random solutions instead of 2.

All three attempts did not outperform SA. By this time the contest was almost over and I was very tired. So I just did some performance optimisations and it took me to 8092 points

I have learnt a lot from this contest.
My favorite post mortems : eldidou and euler

1 Like
#35

Agade - I do not know do symetry of sytuation means that best solution is symetrical too. It is well know in physics that even in case of symetrical environment and physical laws -it is possible that the best solution is not symetrical. It have even special name ā€˜spontanous symetry breakingā€™. In current phisical models ā€˜spontanous symetry breakingā€™ is the reason that particles have the mass (and because you are made from particles - it is the reason that you have the mass :slight_smile: ) Think about ball on other ball. This sytuaction is symetrical regarding rotation around vertical axis but solution with minimal gravitational energy is not symetrical (balls lie on the floor next to each other).

In this case best solution can be symetrical but symetry of the sytuation is not the proof of it.

#36

Finished 48 in Java with 8.6K.
Excellent game, thanks a lot to Magus and Agade, I had a lot of fun to play and wish I would have had more time.
No bug, simple statement, deep game, fun to watch the little robots walking for my kidā€¦ :slight_smile:

I used SA with poor tuning (initial temperature and annealing schedule are almost random numbers).
I added some restarts when Iā€™m stuck for 10K iterations, this helped for ā€œpath testsā€ such as 13 and 28.
@Agade Iā€™m amazed by your restarts after 256 iterations, for me lowering it to even 1K was completely breaking my score.
For the large maps like 22 26 29, I was clearly lacking performance ( 40K on test 30) as my best solution was always found in the last 1% of my simulations.
Iā€™m wondering how much the other Java guys achieved, but I guess itā€™s not only the languageā€™s faultā€¦ even if with such a simple simulation, I donā€™t see a lot of options to be better.

For the validators during such a contest, I think that it was an excellent idea to have the same in IDE & submit during the coding, and then slightly different ones for the final ranking.
Maybe for the final ranking it would have been good to have more tests or to run the set multiples times (and then take average or best, depending on what you want to promote).

Finally, even if thanks to the validators it was not a spam-submit contest, it was sometimes a pain to be stuck by the submit limit, without knowing easily those limits (no idea where theyā€™re documented) and when youā€™ll be able to submit again.
I see a possibility that someone is unable to submit his last version before the deadline because of the limit, that would be sad for him :cry: :stuck_out_tongue:

3 Likes
#37

And how did you guys store history of visited cells? In my submit I use integer hash set of something like 1000x+10y+direction and tracking/updating history was in top of my profiler output. I also tried to use bit array with cleanup using arraycopy from empty array (some java-specific stuff), but it just made it slower. Anyone was able to find something interesting for it?

#38

Each robot has a set of triplets (x,y,direction).

#39

My Robot class has a bool states[190 * 4]; member. When a robot visit a cell i just do states[robot.direction * 190 + cell.id] = true;

#40

I also tried to used a byte[190] array. When a robot visit a cell, I just do
path[pos] = path[pos] | (1 << direction);

But I didnā€™t need to clear/copy it like you mentioned :thinking:

#41

So I just fixed my bug and submitted in multi player version.

Took me like 10 minutes :confused: I score around 8500 which is not great but still better than my 4500ish score in the contest.

The bug was pretty obnoxious compiler default behavior stuff:

unsigned char myByte = 0xff;

The test: ā€œif (~myByte)ā€¦ā€ I expected it to equal if(0) but it was always true probably because of default promotion to int I guessā€¦

It was not hard to find as it implied an immediate and constant issue but I was short on time and was also a bit sleepy at the end.

At least iā€™m quite happy it wasnā€™t a 12k score, I would have been very frustrated lol.

My strategy was pretty simple, I just simulated moves and tried to change direction when a bot was about to disappear, I also randomized the cells and kept best results at time limitā€¦

Iā€™ll try a few different things to see if i can improve :slight_smile:

#42

Hi!

Congrats Magus and Agade for a nice puzzle! I didnā€™t have time to participate unfortunately.

About the auto-submit of codes: itā€™s quite an old feature that was too risky to take care of in such a short time. We realized it during the contestā€¦ Iā€™ll think about it in the following days. We have a larger issue concerning the global competition (contest points vs multiplayer points) that is getting worse with every contest. Iā€™ll unearth the related forum post and relaunch the discussions.

About the contest points themselves, there was a bug and the points have been wrongly awarded. Thanks @papyjo for noticing it.

2 Likes
#43

I use an array of unsigned char[4], each one of them representing the visits of all the robots in a particular direction (UP=0, RIGHT=1, etc)

So:

grid[x][y]->visited[UP] = 1 (in bits 00000001) means robot 0 visited cell x,y in the UP direction
grid[x][y]->visited[LEFT] = 9 (in bits 00001001) means robots 0 and 3 visited cell x,y in the LEFT direction and so on.

To check if a robot visited cell x,y in direction dir I use

if (grid[x][y]->visited[dir] & (1 << robot_id)) { }

To mark a cell x,y in direction dir as visited by robot_id I use:

grid[x][y]->visited[dir] |= (1 << robot_id);

#44

Maybe weā€™ll have the formula modification we ask for years ? :heart_eyes:

#45

And how did you reset state to run a new simulation without cleanup? Or you just throw away this array and take new one from pool?

#46

Oh yeah, this one is deleted. I reset the map and the robot positions/directions only

#47

Hello. Thank you for the great contest.

For the first a suggestion about point calculation. Now you just take sum of results for all final tests as final score. This approach is stimulate to take care only about big tests with many points (where you could gain or lose 100 points at once) and forget about small tests. Nothing is changes for you if your algorithm could not find solution for 100 point in Roundabout and find only for 99 or 95. I suggest to change point calculation in next contests by something like this:
For each test order all results from all participants. Then all who gain top 1 score on this test will get 200 points for this test. All who gain top 2 score will get 150 points. 3rd score - 100 points. All the rest - (50-order of his score).
Such system will stimulate to achieve best results on each test even small one. There was some smart optimizations in A*Craft for small puzzles that could not help in big ones. For example removing arrows in long corridors. Another example is splitting optimization in puzzles that factors on several independent areas. But this techniques did not bring almost anything because they are not work in big tests and effects from them is very little among optimization for big tests.

Now about my solution. I finished 24 with 9,394 points. I used Late acceptance search algorithm with history window of size 8 and restarting after 6000 turns without improvement. As mutations i used changing arrow is single cell. Probabilities of changing to empty arrow is made higher then probabilities for changing to direction arrow. Some arrow directions was excluded from mutations: arrow pointing to void or to opposite arrow.

2 Likes
#48

Where does this information come from ? Did you checked among all the plays in your DB ?
754 seems to be the maximum for this test, am I wrong ?

#49

He said during the contest that he checked the best score for each test cases he found in the database for all submits. So someone submitted a code that does 784 for the 29th test case.