12 8
1234321
....#.......
........#...
...........#
...#O.......
...#........
.......#....
...........#
....#.......
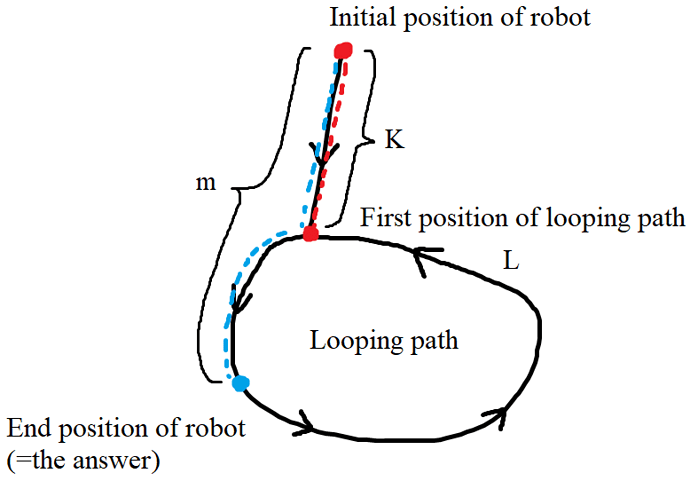
For example: here’s a testcase I cannot pass, because I’m off by 1 step. I don’t include the vector back to start. But if I include these vectors I’ll pass these two cases but fail the infinite loop cases.
These are my cached results of visited nodes. The r,c,and direction or move index and the step. When the robot turns it will not increment the step.
{
‘3,4,0’: 0,
‘2,4,0’: 1,
‘1,4,0’: 2,
‘1,4,1’: 2,
‘1,5,1’: 3,
‘1,6,1’: 4,
‘1,7,1’: 5,
‘1,7,2’: 5,
‘2,7,2’: 6,
‘3,7,2’: 7,
‘4,7,2’: 8,
‘4,7,3’: 8,
‘4,6,3’: 9,
‘4,5,3’: 10,
‘4,4,3’: 11,
‘4,4,0’: 11
}
n = 1234309 totalsteps = 11
1234309 % 11 = 10 additional steps which is incorrect because I'm not including that last vector.
n = 1234309 totalsteps = 12 (including that last vector as a step even though I've traversed it already)
1234309 % 12 = 1 additional step. which is correct which ends up landing me in row 2, col 4 or answer 4 2.
When I do find a loop I would just make the robot remain in position and modulus the n by the total steps of the loop. This may be what’s incorrect(?), but I don’t think so. I believe this is correct logic in just having the robot stay in place, mod n by total steps so we can find out what remaining steps need to be taking by the robot.
Here’s the infinite loop case where I do pass by not including the last traveled vector to a loop.
12 6
4000000000
..##..#.....
...........#
............
............
.#.O........
..........#.
The last vector that I do not include is at 1,3,1 and that gives me the proper mod value.
{
‘4,3,0’: 0,
‘3,3,0’: 1,
‘2,3,0’: 2,
‘1,3,0’: 3,
‘1,3,1’: 3,
‘1,4,1’: 4,
‘1,5,1’: 5,
‘1,6,1’: 6,
‘1,7,1’: 7,
‘1,8,1’: 8,
‘1,9,1’: 9,
‘1,10,1’: 10,
‘1,10,2’: 10,
‘2,10,2’: 11,
‘3,10,2’: 12,
‘4,10,2’: 13,
‘4,10,3’: 13,
‘4,9,3’: 14,
‘4,8,3’: 15,
‘4,7,3’: 16,
‘4,6,3’: 17,
‘4,5,3’: 18,
‘4,4,3’: 19,
‘4,3,3’: 20,
‘4,2,3’: 21,
‘4,2,0’: 21,
‘3,2,0’: 22,
‘2,2,0’: 23,
‘1,2,0’: 24,
‘1,2,1’: 24
}