Never mind, I had the formula to check if it’s a square messed up ![]() It works now
It works now
Think about how many points define the remaining square coordinates (more or less) uniquely. Brute-forcing by nesting four loops will definitely be too slow!
If you are stuck on getting the code to run faster after this, it may be helpful to know that it is much faster to determine whether an element is present in certain types of objects than others (O(n) vs O(1)) – so which type of object you store the points in is important. I don’t want to give too much away, but hopefully that should enable you to find the necessary information to solve this puzzle for the larger cases too!
Thank you for your advise.
For other seekers one more advise: “Make your program easier,delete unnecessary conditions”.
I get 6 for that input (numbers are index of the peg in the input):
(0, 1, 3, 4)
(0, 2, 6, 8)
(1, 2, 4, 5)
(1, 3, 5, 7)
(3, 4, 6, 7)
(4, 5, 7, 8)
6 squares:
{X=0,Y=0} {X=1,Y=0} {X=1,Y=1} {X=0,Y=1}
{X=0,Y=0} {X=2,Y=0} {X=2,Y=2} {X=0,Y=2}
{X=0,Y=1} {X=1,Y=1} {X=1,Y=2} {X=0,Y=2}
{X=1,Y=0} {X=2,Y=0} {X=2,Y=1} {X=1,Y=1}
{X=1,Y=0} {X=2,Y=1} {X=1,Y=2} {X=0,Y=1}
{X=1,Y=1} {X=2,Y=1} {X=2,Y=2} {X=1,Y=2}
wow great thanks!
Getting hard time to understand the instructions,
Can someone give a good example of squares count?
For the next input:
9
0 0
0 1
0 2
1 0
1 1
1 2
2 0
2 1
2 2
Does it output 5?
Hey,
currently I using brute force - taking all 4 points combinations (using 2 for loops) and checking if they make a square (every combinations is unique).
Of course I’m getting timeout with 500 points, and suggestion how to solve this puzzle?
Read the comment of Monoterpene and next comment after him
trust me I read all comments before I post
I’m not sure what you mean by checking all 4-point combinations with 2 for loops – if this is by picking all 2-point combinations (possible at that point) within each of the loops, it seems equivalent to nesting 4 loops. As I hinted at above, you can get away with looping over fewer than 4 points (but still making sure that the other points are in the allowed set).
Apologies if I’ve misunderstood what you mean.
Which language are you using?
I’m using javascript,
@Monoterpene I’m looping over all the subsets (that’s why it’s 2 for loops),
I think I missing some “unnecessary conditions” but anyway I don’t think it will help, maybe there is another approach?
If I understand correctly that you are generating all combinations of 4 points from the given set, and then testing whether they form a square, your code will be too slow for the large-number-of-points cases. Yes, you need to find an approach that gets away with looking at fewer combinations.
Further hint: if I give you the coordinates of two points in the plane, how many squares have those two points as their vertices? Can you use this?
Love this puzzle !
It looks simple at first, but has couple of "gotcha"s.
One is the identification of the squares
The other is the optimization needed for bigger sets.
Monoterpene already provided all the hints necessary
Hi,
I think a test with non axis-aligned squares and a reasonable amount of points should be added to the test set, such as the example proposed by Dennis Vash. I missed the point despite it is written in the text, and I spent time looking at my fault. At first I disliked this puzzle for that, and I think an easy-to-handle example would help beginners and non-fluent English speakers to get it all, and people like me ![]() .
.
I have to go back to the puzzle, the non aligned squares make it much more exiting now.
Thank you
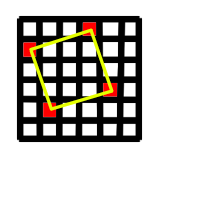
I got 5 and by visual count and by my current algorhitm I also got 5, where is 6th square? I mean purely visualy. Its 3x3 array, so there is 4 disctinct 2x2 squares and 1 3x3 square. I most likely struggle to get assigment right, cant find 6th square :] Please help!
You’re missing the last, non-axis aligned one:
0 1, 1 0, 2 1, 1 2
Oh wow, I didnt thought of this, so diagonal sqaures are also in equation. Thank you very much.
Cheers.
So, square like this would be also in possible squares?