[Community Puzzle] Encounter surface

Puzzles
#1

https://www.codingame.com/training/hard/encounter-surface

Send your feedback or ask for help here!

Created by @BLANC,validated by @java_coffee_cup,@Irioth and @luke-guyton.
If you have any issues, feel free to ping them.

#2

How can you determine the shape when you don’t have the order of the vertexes their could be multiple cases. Like the example given, the first shape (the one that have 5 vertexes) has at least two possibilities

#3

One way of doing it : compute the center of all the points, arbitrarily choose one of them as the first one, then rotate the line “center - first point” from 0 to 360°. Everytime the line hits another point it’s the next one. You end up with a list of the points sorted counter clock wise starting at the first one you chose.

Edit : From the constraints, “The polygons representing the armies are convex polygons”

3 Likes
#4

You might want to solve the windmill problem before (https://www.codingame.com/training/medium/windmill-problem), it’s about finding the next point when rotating clockwise, so it’ll make you work on this specific task.

#5

Hmm interesting the way I did it was to simply walk from one randomly chosen point to the next closest one and then to the one closest to that(removing the first one) Rinse and repeat until there are no points left . Given the restriction that the polygon is convex I thought this should create the correct shape.
Am I missing some cases her ? Or does this end up being the same as the windmill approach ?

1 Like
#6

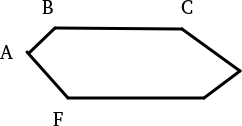
This “nearest point” approach can make error. The nearest point is not always the real next point in a polygon

Start from A, nearest is B. B’s nearest is, you want it to be C but it turns out F.

.img-1

3 Likes
#7

Is it too much of a hint to mention Sutherland–Hodgman?

1 Like
#8

I did it by computing the barycenter of the vertices (let’s call it G), and then computing the angle between the horizontal axis G->horizontal, and each vertice GV. And then, simply sort by angle.

1 Like
#9

I tried two different approaches and all tests succeed in the IDE environment, however for both the test Validator Great battle fails as only test in the submission (83% score). I cannot see what is wrong in my approach. Am I the only one experiencing this?

First approach was counting all coordinates between min and max coordinate which are inside both polygons (with a scale factor applied to improve precision). area = insidePoints + (onSidePoints - 1) / 2

Second approach was to determine the intersection polygon using Sutherland–Hodgman and calculating the area of this polygon using linear algebra.

1 Like
#10

oh gosh yeah I didn’t think about that back to the drawing boards :slight_smile: I have to say I like this problem its something super trivial to do with pen and paper and a human mind but very challenging to put into code…

Well thanks for the input :slight_smile:

#11

The way i solved it was to compute the intersection polygon, by finding:

  • the vertices from one polygon contained in the other polygon (in both ways)
  • the intersection points between sides

One thing that made me fail consistently is that the subject talks about “rounding”, but in fact, it is ceiling (rounding at the upper int).

1 Like
#12

I have the same problem but, for me, it’s the “Validator Side superposition” that fails…

I did like @jfaixo said, but had problems of precision in calculating the intersections and detecting whether a point was inside a polygon or not.
I fixed them by using another algorythm and using the sum of the angles (that should be 360 if inside the polygon).

But, I don’t get what I missed on the last validator.
It’s probably a limit case, but which one ? Do you have any idea ?

#13

I verified that it is not a rounding problem by adding +1/-1 to the answer and submitting, both still fail for the specified test case. Also the algorithm runs within 100 ms (should be fast enough).
It’s weird that two different algorithms fail on the same test case while the IDE test cases all succeed. Because you cannot see the output of the validator test cases it’s hard to figure out what is going on.

1 Like
#14

Not specific to any test case, a possible tricky situation is to have some vertical and some horizontal lines (with slope 0 or infinity) in the polygons. When two polygons overlap, some points can overlap. Some lines can fully or partially overlap. All these situations may need special handling in calculation.

1 Like
#15

For sorting the vertices I created a simple algorithm that doesn’t use center, angles, goniometric functions at all. It just uses vector product of couple of points and switches them:
i=1…len(v)-2 {
j=i+1…len(v)-1 {
v[0]v[i] Ă— v[0]v[j] < 0 ? switch(v[i],v[j])
}
}

#16

Was fun to solve it using just vectorial products,
not a single division nor any goniometric function used!

#17

Is it too much of a hint to mention Sutherland–Hodgman?

Not too much, I would say: “exactly the right amount of hint” for me :slight_smile:

#18

Is there something special about the “Validator Real Case”?
My program passes all tests in the IDE, plus some custom tests with edge cases not covered in the default tests. It’s been several days I’m working on it, but my score is still 83% :thinking:

#19

Rewritten from C to Lua. Same algorithm. Passed 100% :thinking: