https://www.codingame.com/training/easy/knights-jam
Send your feedback or ask for help here!
Created by @Niako,validated by @JBM,@bbb000bbbyyy and @dwarfie.
If you have any issues, feel free to ping them.
Looks like that it is another breed of 3x3 sliding puzzle. Nice.
Please help me to understand the puzzle. If any number can jump to the empty cell, how can be unreachable the order from any setting?
Why is test case #7 unreachable, it’s reachable in one move if following chess rules right ?
Which one move would that be?
my bad, I parsed it wrong. I thought there only needed to be an empty spot on the correct place and the numbers were irrelevant.
Hello,
I’m quite new on CodinGame and a bit puzzled regarding Validators. Are they specific to each puzzle or a set to check general coding rules?
Besides that, I’m surprised to get only “Ok/Ko” results without any message telling what’s wrong. If you don’t know what’s incorrect, how could you get a chance to fix it?
Is there something I missed (I searched for validator in forum but didn’t get anything helpful for me)?
What is the purpose of those validators?
Thanks.
@Anton-Roneo Validators are hidden testcases that are used to validate your submission. Each public test (that you can see in the IDE) has a corresponding validator which is supposed to be of the same “complexity” and to cover the same “kind” of case. Ideally, when you pass all tests, you pass all validators. But sometimes a code with small mistakes can pass all tests and fail at one of two validators (or the opposite).
If you pass all tests but fail at some validators of the Knight Jam puzzle, then you can send me your code in PM, I’ll have a look at it.
2 Likes
backtrack works correctly
I simply dumped the solution, and it took me less then 100 lines. Not good.for a problem.
@Natalka1122 It can indeed be hardcoded, even though it’s not very interesting to do so, and the way you did it still requires some insights into the puzzle. But it was initially intended as a Clash of Code, then resubmitted as an easy puzzle, then moved to medium as it was considered a bit too hard for beginners, so, yeah…
1 Like
Yeah, to write my code I had to write another program that explored the problem and finally it turned out - generated my solution =)
1 Like
I love this puzzle! The more you analyse it, the more it simplifies… and the more it simplifies, the more shortcuts you see. The final solution can be very elegant indeed : )
To anyone about to attempt this puzzle, I strongly recommend spending some time with a paper and pen, looking at how the knights move individually - and, also, how they behave as a group.
5/5 for this puzzle. Well done Niako!!!
1 Like
I solved it with a BFS, but i think there is an easier way … is it true ?
2 Likes
There is another solution, but I’m not sure if it’s actually easier. It’s computationally easier, but it requires some insights into the structure of the game.
Spoiler
The goal state is:
123
456
78.
There are 2 possible state-move pairs that lead to this state. For the sake of demonstration, we’ll look at just one of them: moving piece #2 in the following state:
1.3
456
782
Again, there are two possible state-move pairs that lead to this state: moving piece #2 in the goal state and #7 in the following state:
173
456
.82
If we keep going in this way, we’ll find out that moving pieces #2, #4, #3, #8, #1, #6, and then #2 (8 moves in total) in the following state leads to the goal state:
874
251
63.
Observe that this set of moves effectively makes the pieces move in the following manner while keeping the empty square at the same position:
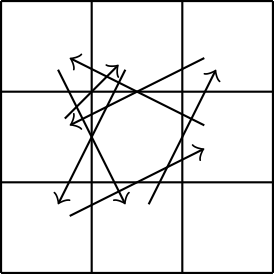
This forms a cycle of length 7. This means that if we go further back 6 × 8 = 48 moves (that would be 7 × 8 = 56 moves from the goal state) then we’ll be back at where we begin – the goal state. At this point, we have identified every single state that could reach the goal state.
Therefore, if you draw the state transition graph of the game, you’ll get a cycle of length 56 (here we only consider reachable states). Hence, solving this problem comes down to finding if and where the given state is in the cycle. You can do so by analysing the positions of the pieces and the empty square or listing out every single reachable state and build a lookup table.
(Update: Anti-spoiler (thanks @Niako))
1 Like
@abt8601 Nice answer! But could you hide all that in a collapsible “Spoiler” block?
Like that
[details="Spoiler"]
This text will be hidden
[/details]
Thank you for the explanation 
2 Likes
Really cool puzzle! Had a lot of fun. Forcing you to analyze outcome. Solution can be easy.
1 Like