Rank: 16th Legend
Language: C++
First, it was a very nice occasion to commit whole 11 days to a CodinGame contest. I once reached 1st place on the 9th day, which was a great experience. Thanks CodinGame and Société Générale for hosting the contest!
I used a combination of brute-force-like search and linear evaluation function which is learned by reinforcement learning.
While many other participants applied heuristic “rule-based” choices (like one in MCTS), the parameters on my evaluation function was completely detemined by a computer program.
Overall Strategy
First of all, the important point of this game is that:
- The chain of actions from MOVE to RELEASE differs so much by slight difference of one choice or slight difference of one card. It is very “discrete” in this sense.
- However, when the next player draws 4 cards, it will be smoothed out. It is true that there are lucky draws and unlucky draws, and one difference of drawn cards will change everything. But in the sense of expected win-rate, all possibilities are condensed, taken average, and becomes “continuous”.
I thought that the contrast of discreteness and continuousness was the key to the problem. This trait gave me the insight that:
- We need to brute-force (or search like MCTS) chains of actions from MOVE to RELEASE, to find the best action, because evaluation can be difficult.
- But it can be easy to evaluate “terminal phases”, which are the phases after RELEASE and before drawing 4 cards.
This became the blueprint of my algorithm for this game. Then, all I need to do is to make the brute-force-like search algorithm and a good evaluation function of terminal phases.
Part 1. Search
In fact, the number of chains of actions from MOVE to RELEASE is not so large. For example, there are about 200 chains of actions on the first turn (one of them is MOVE 5 → CI 8 → WAIT).
It turned out that we can search about 10,000 chains of actions in 50ms time limit. So, brute-forcing them is possible and can find the “true” best-evaluated action.
If there are many TRAININGs and CODINGs, many branches will occur and the number of states to be considered will increase exponentially, which may exceed 10,000. For coping with such cases, I used the following search algorithm.
- Until reaching terminal phases, repeat choosing an action randomly among which the next state is not “everything is searched”.
- If the state become “everything is searched”, the true evaluation is calculated so we don’t need to search all states. Otherwise, we calculate the evaluation based on searched results.
- If the root state become “everything is searched”, it means we completed the brute-force and we can quit searching.
This algorithm enables to brute-force (or nearly brute-force when the number of states is large). The reason why I did not use MCTS here and applied almost-pure Monte Carlo choice is the “discreteness” of this phase.
Part 2. Evaluation Function
As the terminal phases has “continuous” traits, I thought that the win-rate can be predicted by an easy formula. For example, we can imagine something like the following:
- One technical debt decreases win-rate by 3%.
- One automation of bonus card increases win-rate by 20%.
- A person who is at location 0 is favored to win by 15% against the person who is at location 7.
So, what can be done in general? The game states can be divided to many components - score, location, the number of each cards, the number of each cards automated, the skill levels, and so on. I tried to assign “advantage weights” for each components.
Let’s go in details. Suppose the advantage weight of one automated bonus card is 1.1. If a player has 5 bonus and the other has 2 bonus, the player has +3.3 advantage, which is translated by 1/(1+exp(-3.3)) = 96.4%.
In general, I intuitively used logistic function to translate the advantages to win-rate (like chess). Let (w1, w2, …, wk) be the advantage weights of each component, and (x1, x2, …, xk) and (y1, y2, …, yk) be the values of components for each player, the advantage is calculated by A = w1(x1-y1) + w2(x2-y2) + … + wk(xk-yk), which is translated to win-rate 1/(1+exp(-A)).
Part 3. Machine Learning
I used TD-learning to assign the advantage weights. 20,000 self-plays were done using the epsilon-greedy method (70% optimal choice, 30% random choice).
The “temporal difference” in TD-learning is the difference between the estimated win-rate using pure evaluation and the estimated win-rate using brute-force-like search towards the next terminal phases.
One self-play took about 100 turns on average and took about ~0.2 seconds in the end. Overall, the 20,000 self-plays were done in about 2 hours using a single thread of Intel Pentium Silver N5000 CPU (1.1 - 2.7 GHz).
How the AI learned to play?
At first, all advantages weights are set to zero. So, everything was random-like at first dozens of games.
At about 1,000 games, the AI learns the efficiency of “CI 8” and the first player becomes likely to win (like 70%). However, at about 5,000 games, the second player knows to “MOVE 2 → DAILY_ROUTINE” at the first turn, then the win-rate becomes even against first player and second player.
Gradually, the AI knows the efficiency of CI-ing normal cards and the knowledge of locations, and became more faster to finish the games.
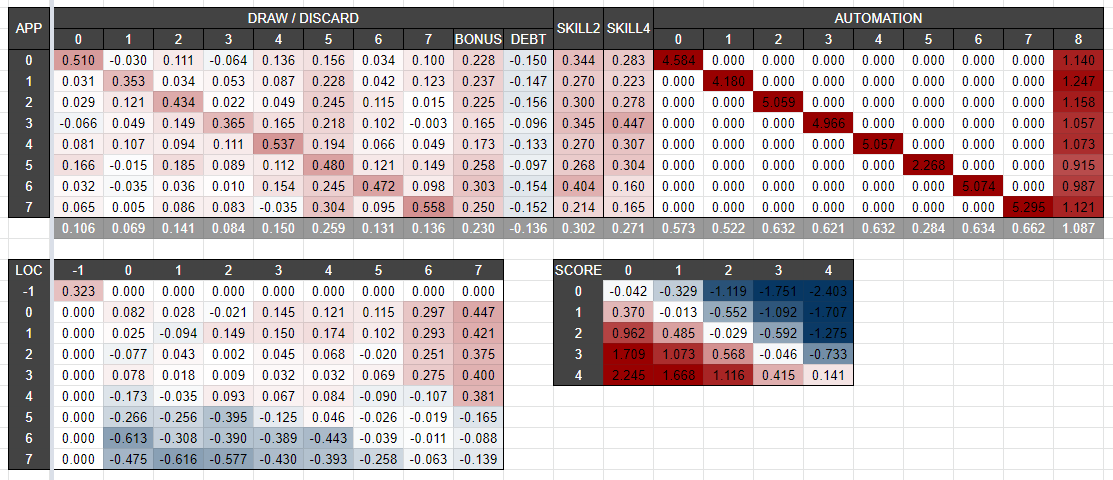
The Advantage Weights
Some part of calculated advantage weights (for the first player) are given below.
I think that this yields some lessons for this game. For example:
- One bonus card increases ~5% win-rate.
- One technical debt decreases ~3% win-rate.
- The strength of cards are 5 > BONUS >>> 4 = 2 = 7 = 6 > 0 > 3 > 1 >>> TECHNICAL_DEBT.
- One automation of bonus card increases ~20% win-rate.
- One automation of normal card (except 5) may increase a decent win-rate, depending on required skills in the remaining apps.
- When the turn begins (and before MOVE), “player is in location 7 and opponent is in location 1” is the worst, while “player is in location 0-4 and opponent is in location 7” are the best.
- The fact “player’s score is 4 and opponent’s score is 0” increases ~50% win-rate just by alone.
Finally, this was really an interesting game to tackle. Thanks!
Without Referee, it was very difficult to develop a correct simulation. I passed through a few dead ends, before i wrote, what need to me.
(moves).
Solid gameplay and complex rules, just as I like it 
)
)
