gold 421st java
i appreciated the novel game concept
algorithm notes
wish i could give more energy to these contests, it is fun. good game all and i look forward to reading your posts.
Just local self-play against some of my other bot versions. Then, for each turn of each match check the state of the minigames and their end result. Training input is the mini gameâs state, and training output is 3x a 0 or 0.5 or 1, depending on the final medals of that mini game.
The goal was to get better eval than my manual attempt (which wasnât bad either, got me to #1 for several days). I think in the end it gave about 65% win rate against manual eval.
Here is a write-up for Frictionless Bananas (Legend League, 46th place): Frictionless Bananas - CodinGame Summer Challenge 2024 (Olymbits) Entry
Thanks to CG to keep hosting these contest, the game was interesting !
I ended #20 Legend, with Rust 
of course !
Iâll not elaborate much as my approach is very similar to all the other ones above. In short:
, and some experience in mcts & bot implementationâŠ
, that allowed to offline test bots. In this game, local improvements have almost always translated in ranking improvements in the arena. A true compass while at sea#31st Legend, C++ (my best ever result)
First of all, congratulations to all participants and thanks to CG for organizing the event. As many other competitors, I suffered from occasional timeouts which I could not relate to any bugs on my side. Apart from that, things went smoothly. I particularly liked that the event lasted two weeks which gave me enough time for coding while dealing with real life constraints. For the same reasons, I appreciate that leagues were opened at a steady rate.
I liked the game topic. CG guys are insane!
My bot is deceptively simple:
It is very important to include skating with random gpus in the simulation (thanks Thyl for the tip). I have no real explanation for this but my bot gained + 4 TS with it and this promoted me to Legend with +1 against the Gold Boss. Fun fact, I had a huge bug: the skating gpu was not random but repeated the current value. Randomizing it is better but not that much.
In retrospect, I should have paid more attention to rollouts: instead of using purely random moves, I should have incorporated randomly chosen good moves for diving, hurdles or archery.
86th, 24th in gold, C#
I used the greedy method.
For each mini-game, a (rating * weight) was calculated and added together.
Each game is evaluated based on the number of losses and draws, with the best moves being made.
Games with fewer medals already earned and games nearing the end have a higher weight.
(More information, Japanese language)
https://inaniwa.hatenablog.com/entry/2024/06/25/180350
And thank you for hosting the contest.
Fighting bots that only focused on one minigame wasnât much fun,
but the judging was solid and I had fun competing in the Gold League.
#6 Legend
I wanted to be a bit original with my search algorithm, and the thought I started with is that I really, really disliked the idea of UCT forest/smitsimax for this game and I wanted to fix it. The reason why I thought smitsimax wouldnât do well in this game (and hey, I beat all the smitsimaxers, so I guess Iâm right) was the diving minigame: often, my opponentsâ 2nd move (continue the diving streak or not) will heavily depend on whether I chose to dive in my 1st move, and in those cases, the results of smitsimax would probably be garbage.
In an attempt to fix this, I combined smitsimax and DUCT - I still use three separate trees like smitsimax, but instead of using one tree per player, each tree was a DUCT-like tree for a pair of players. The selection part still happens just like in smitsimax, but each player sums up the UCT formulas from their 2 trees, and instead of random rollout, I evaluate minigames in progress after one tree expands (skating only at depth 1; rollouts worked worse for me). I hoped that with this, I could reach higher depth than a DUCT would, without losing the player interactions like smitsimax does.
Of course, it backfired.
Consider a game state where 2 players are 3 spaces away from the hurdles minigameâs goal, and a starting diving minigame with the first action not being RIGHT. This is an example of a prisonerâs dilemma - if both players agree to split the gold medal one turn later, they can also both start their diving streak and not fall behind the third player in that minigame, but thereâs also the risk of one player just getting the hurdles gold medal in one turn. My algorithm consistently converged to cooperating with the other player and it was getting consistently âbetrayedâ on the leaderboard. My attempts to fix this were only partially successful: the medals gained by the opponents were already in my eval, decay made the bot play much worse (maybe it messed with the weights of different medals), adding a bit of randomness to the tree node selection did help a bit but didnât solve the problem completely, paranoia and contempt did not work at all.
The main problem with this, even when I managed to find some workarounds to the issue, is that my selfplay became mostly useless, because any bot that switched to betraying more often would be outcompeted by the cooperating âfriendship forestsâ in my local arena, and thus my attempts at parameter fiddling based on selfplay winrate did not do well - which was when I originally found out whatâs happening with my bot.
Not having reliable selfplay meant that I had to somehow come up with an evaluation function for unfinished minigames. I assumed that the number of spaces a player advances in skating and hurdles would be approximately normally distributed, and therefore the probability of one player being overtaken by another would be a sigmoid function of the playerâs lead. I downloaded a lot of top playersâ games using the CodinGame API to verify that this is indeed true and to be able to find some functions that approximate the average winrate relatively well. This approach also worked for archery (the sigmoid is a function of distance from center divided by average wind speed) and diving (function of the number of turns that the player ahead would need to avoid diving at the end of the game to be overtaken by the player behind). The approximation gets imprecise when there are only a couple of turns left in the minigame which would be a problem for the skating evaluated at depth 1, so I also created a dataset of win probabilities (~1000 data points) for the skating minigame from a given game state close to the minigameâs end (now many spaces a player is ahead, each playerâs risk, turns left). For illustration, hereâs the relation between a playerâs lead in hurdles, his position, and the average game result, based on ~10000 legend league games:
#202 Global Rank, reaching Gold league
During the recent CG challenge, I had the opportunity to code my bot using C++ and implement the Monte Carlo Search Tree (MCTS) algorithm. It was my first time working with MCTS, and although I didnât fully grasp all its intricacies, I managed to make progress by black boxing certain parts of it.
In my implementation, the expandable moves from each node were limited to my four possible actions. I didnât take the opponentâs moves into consideration, so during the rollout phase, I only simulated my player until reaching the GAME_OVER state in all of them (ignoring the Skating mini-game).
At the terminal state, I scored each mini-game as follows:
There were certain states where I ignored the mini-games because my focus was on finding the next best action. For example, I disregarded the Hurdle Race if my player was stunned or if the best turns I could make would exceed 100 turns. Additionally, if I was already guaranteed a winning or losing position, I didnât consider the Hurdle Race either. As for Archery, I used Dynamic Programming (DP) to determine the best achievable outcome for each action. If the best outcomes were relatively close to each other, I ignored it. Furthermore, I only considered Archery in the last 8 to 10 turns, as it was often guaranteed to reach the center within 7 turns. In Diving, I ignored it if one of the players had a guaranteed win.
I assigned a value from 0 to 1 to score each mini-game based on how favorable or unfavorable the state was. Then, I multiplied the score for each mini-game by their respective weights, which were calculated based on the medals I had in each mini-game. I gave more priority to the mini-game with fewer medals, as winning in that mini-game would have the greatest impact on my final score. I also took into account how many turns were left until the mini-game ended, allocating a small portion of the weight accordingly.
Initially, I was satisfied with my botâs performance. However, towards the end of the contest, I reached a point where I couldnât think of any further improvements. I realized that considering the opponentsâ actions would significantly enhance my botâs performance, but I struggled to implement it with MCTS. The challenge stemmed from the fact that it would result in 64 child nodes for each state, and I had difficulty selecting the next state. While scoring the terminal state was clear to me, the selection process proved to be a bit confusing. Furthermore, in terms of complexity, I was only able to perform around 1,000 iterations when working with MCTSâs 64 child nodes, while considering only my playerâs moves allowed me to run up to 10,000 iterations.
I would like to express my gratitude to CG for organizing such an amazing challenge! I would also like to thank the 1337 school community, of which I am a student at. Congratulations to the school for achieving the second place in the schools ranking.
If I could upvote this 10 times I would. Thanks for the NN details!
â Great insight and analysis. I didnât think to look for that pathological failure point in the local benching
#61 Legend
Bottom Legend, I barely reached it on the last day, I used the genetic algorithm this time because I am more familiar with it from past contests, It was slow and I think it was not the right tool for the job.
Hereâs how it went for me in this contest, I reached bronze as quickly as possible and started to implement a working simulation added some heurists to reach silver, and then I started working GA.
itâs a regular genetic algorithm the major difference is that instead of having one population I have 3 each one for each player, and in each iteration, itâs a playerâs turn to develop its population against the best chromosome from the other two playersâ population, this way I can see the behavior of letting some game because it guaranteed to be winning or focusing on the specific game because it will contribute to the score more. the limit is the scoring function.
How it looks like:
#[derive(Debug, Clone)]
struct Chromosome {
genes: VecDeque<Direction>,
fitness: isize,
}
#[derive(Debug)]
struct GeneticAlgorithm {
population: [[Chromosome; POPULATION_SIZE]; NUMBER_OF_PLAYERS],
}
impl GeneticAlgorithm {
fn run(&mut self, game_state: &GameState) {
self.init(game_state);
let mut player_id: usize = 0;
while <time to tun> {
self.selection(game_state, player_id);
self.crossover(player_id);
self.mutation(player_id);
player_id = (player_id + 1) % NUMBER_OF_PLAYERS;
}
}
}
my scoring function at first was simple I just calculated the game score with medals and considered the final state of each minigame by adding an additional score if the player was close to the objective in each minigame. That was enough to get me into gold to 200 ranks, then I tried many other things without result until I included the opponentâs score to the scoring function in a way that the score increases if the sum of opponentsâ scores is lower, I donât know how this worked but it gets me consistently to the top 10 gold and I get pushed to legend at the end.
this was a fun contest overall, looking for the next one.
Thanks to Codingame again for this great Mind Trap competition.
Congratulation to all competitors to gather 10 days for this new competition and give high values to our legends.
Hi,
18th Gold here.
Big shoutout to the whole CodinGame team for preparing another bot programming contest. I really like the format and canât wait for every next edition.
From the first look I didnât like the game. Big part of the contest is to sit and watch how my bot is doing. This time that part was taken from me. It was almost impossible to track what is going on just by looking at the game.
Nevertheless I dived into the abyss and started coding. The game was very easy to understand, we didnât have to analyse the game code to understand the logic. After a while it was very pleasure to optimise the strategy to get as much points as possible.
One hint for the implementation is to keep the whole sequence of moves in one variable (instead in the container), where each consecutive two bits keep value for a single move. For me it simplify (and speed up) the whole process a lot.
Congratulations on making it to Legend! Your contest journey is really inspiring. I tried using genetic algorithms (GA) like you did at first, but later on, I switched to MCTS. Sadly, switching didnât work out as well for me as I had hoped.
This contest was very interesting. Thanks to Codingame again for this. Here is what chatGPT said about my code 
:
Mastering the Challenge: A Comprehensive Strategy for CodinGame Competitions
Participating in CodinGame challenges is not just about writing code; itâs about crafting intelligent strategies to outperform thousands of other programmers. In the recent CodinGame challenge, where I secured the 169th position out of 5237 participants, I employed a sophisticated approach that combined algorithmic optimization, modular design, and simulation techniques. Hereâs a detailed breakdown of my strategy and how it helped me achieve this remarkable rank.
Overview of the Challenge
The competition required participants to play four different video gamesâHurdle, Archery, Skating, and Divingâsimultaneously using a single controller. The challenge was to defeat two other adversaries by managing these games effectively.
Key Elements of the Strategy
Preparation and Optimization
Data Management
Initialization and Input Handling
Game Simulation
Evaluation of Moves
Solution Generation and Mutation
Simulated Annealing
Brute Force Approach
Achieving Success
By combining these elements into a cohesive strategy, I was able to efficiently manage the complexity of playing four games simultaneously. The key was to balance between exploring new solutions and optimizing known good solutions. This strategic balance helped in maintaining a competitive edge throughout the challenge.
Conclusion
The key to success in CodinGame challenges lies in balancing algorithmic efficiency with strategic problem-solving. By leveraging advanced optimization techniques, creating modular and reusable code, and employing sophisticated algorithms like simulated annealing and brute force, I was able to secure a top 3% position in a highly competitive environment. This strategy not only highlights the importance of technical skills but also the necessity of a well-thought-out plan tailored to the specific demands of the challenge.
3rd place overall
Iâd like to thank CodinGame and Fiverr for organizing and sponsoring this exciting competition. I liked it a lot!
Solution
My bot was based on Decoupled-UCT. Its tree search and node selection algorithms were borrowed from AlphaZero, but its value/policy evaluation functions were hand-crafted ones. I chose the design hoping for a future transition to RL-based NNs (real AlphaZero), but it remained to be a future work until the end of the competition.
Details:
Minor details about node evaluations:
#1
For such short contests, the most important thing is fighting with time and constantly improving the bot. I had a hard time keeping the tempo. I must say the term around the end of the (pre)school year is unfortunate. Although, it is not as bad as the term including Christmas, which is one of the worst options.
Thanks to the organizers, great idea for a game.
Congrats to @reCurse and @Nanaeda for the excellent competition!
Thanks to @aCat, @gaha, @surgutti, and @Zylo for our discussions and sharing ideas.
The game is interesting yet difficult to play, and the rules in the referee were a piece of cake (compared to the nightmare from Fall Challenge 2023). It was possible to get the proper engine in just a few hours, and there was space for its further nontrivial optimization.
The algorithm is a variation of DUCT, mostly fully decoupled, which is called Smitsimax here. In the basic part, there are three independent trees of the players of branching 4, but this is extended around the root. The crucial parts are bizarre management of decisions in iterations based on the number of samples and optimizing a lot.
The fully decoupled DUCT is fragile and exploitable, but I supposed that the budget is too small for a more fancy algorithm. Indeed, the number of iterations strongly affects playing strength and the bot would still improve with more iterations.
Furthermore, the behavior varies depending on the time budget and requires tuning for a specific limit; this concerns mostly the things related to exploration. The fact that there were two different processors further complicated it, so I ended up with experiments with two respective budgets, to ensure that things worked good with both. The next step could be providing two separate tunings, but there was no time for that.
Efficiency matters a lot. The following are the results of the final bot with its two previous versions (99% CI). The final bot has doubled, normal, and halved the time budget, respectively.
MSz[time 200%] vs MSz(v-1) vs MSz(v-2): 57.91% ±1.0 : 48.27% ±1.0 : 43.82% ±1.1
MSz[time 100%] vs MSz(v-1) vs MSz(v-2): 54.93% ±1.0 : 49.55% ±1.0 : 45.53% ±1.1
MSz[time 50%] vs MSz(v-1) vs MSz(v-2): 49.94% ±1.0 : 52.12% ±1.0 : 47.95% ±1.1
The strategy for simulations (rollouts) is to use a policy, which is a chosen minigame that the player wants to maximize. The policy is chosen by weighting minigames depending on the current and predicted scores. It is kept for the next turns until that minigame ends or becomes fully determined, which means the outcome for that player will not change anymore regardless of the actions. Choosing an action is taking a random one from the best ones for this minigame. The best actions are hardcoded by a set of very simple rules. Stunning (in hurdle and skating) does not disable the policy, but then the player temporarily chooses another minigame and makes a best move for it. This simulation part dominates efficiency; the key is to keep it simple and fast. More sophisticated methods worked better sometimes, but not in the timed setting.
When a minigame ends, the next edition is generated, with the same distribution as in the referee. However, each minigame is generated at most once in a simulation, except for skating, which is not generated. When the generated minigames end, the iteration finishes. The scores are completed with predicted scores from future minigames, depending on their expected number of remaining editions.
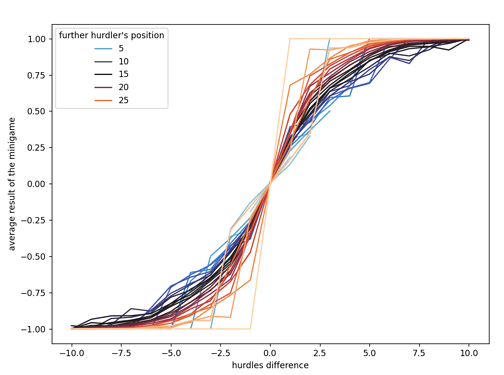
These numbers are easily calculated exactly for archery, skating, and diving, whereas for hurdle it was obtained from massive experiments with already good agents.
For most nodes, the trees are fully decoupled, which means there are only 4 children for the playerâs actions. However, we can branch also on the opponentsâ actions, which gives 16 possibilities, and on the skating order, which gives 24. I do not want to consider branching on possible generated minigames.
The branching on opponentsâ actions is taken in the root, so the branching there is 64. For skating order, a separate tree of a small depth is managed. The latter tree is used for decisions only after gathering a certain number of samples.
The important issue is to take only quality actions in simulations. First, an action is decided by UCT only if the number of samples reaches a certain threshold; otherwise, it uses the policy as above. This gives similar effects as mixing UCT with heuristic values but avoids that expensive formula. Then, there is a surprising mechanism: In contrast with the usual UCT, deciding by the tree starts from a very small exploration, thus mostly based on the choices made previously with the policy. I think this helps by keeping the statistics of the node of relatively good quality. The exploration reaches its normal formula after a certain threshold of samples, which happens only for a small fraction of the nodes at the top.
The final bot performs better when the available budget is smaller, which is mostly the result of the described threshold mechanisms employed in the latest versions. The following are the results with altered budgets but fair â the same for all agents.
[ 200% time] MSz vs MSz(v-1) vs MSz(v-2): 54.27% ±1.0 : 50.21% ±1.0 : 45.52% ±1.1
[ 100% time] MSz vs MSz(v-1) vs MSz(v-2): 54.93% ±1.0 : 49.55% ±1.0 : 45.53% ±1.1
[ 50% time] MSz vs MSz(v-1) vs MSz(v-2): 56.13% ±1.0 : 49.61% ±1.0 : 44.27% ±1.1
[ 25% time] MSz vs MSz(v-1) vs MSz(v-2): 59.52% ±1.0 : 49.28% ±1.0 : 41.21% ±1.1
[ 10% time] MSz vs MSz(v-1) vs MSz(v-2): 65.74% ±1.0 : 45.78% ±1.0 : 38.48% ±1.0
[:-) 1% time] MSz vs MSz(v-1) vs MSz(v-2): 74.45% ±0.7 : 72.17% ±0.7 : 3.38% ±0.4
The branching and thresholds are specific to the time limit. For example, increasing branching besides the root seems to be better under a larger time limit, but worse otherwise.
[200% time] MSz-IncBranching vs MSz(v-1) vs MSz(v-2): 55.04% ±1.0 : 50.93% ±1.1 : 44.03% ±1.1
[100% time] MSz-IncBranching vs MSz(v-1) vs MSz(v-2): 53.32% ±1.0 : 51.36% ±1.1 : 45.33% ±1.1
As the number of iterations is crucial, optimization is essential. There are many tricks measured precisely to give a speed benefit.
The funniest part is precomputing all possible hurdle maps. Then generating a hurdle minigame boils down to get a random id from 1280 possibilities (some are repeated just to ensure the proper distribution). Furthermore, each map is already solved, hence getting the best actions and applying them is essentially done by one lookup and checking the stun.
The average numbers in the second turn over 10 runs on CG haswell:
Iterations: 5 264.6
Game states: 176 527.5
Tree nodes: 15 989.8 + 1 041.3
UCT calculations: 64 241.7
Probabilities: An estimation for an unfinished minigame assuming random moves. Not that such probabilities are useless, but too costly compared to greedy decisions, and maybe not as realistic estimations, since the agents do not play randomly. Probabilities require more complex operations and/or big arrays, which are slow to access.
Weighted moves: The benefit of using a policy is not only imitating a realistic play but also in terms of efficiency â in most of the turns, we do not have to even look at the possible actions for the other minigames. Weighting moves or weighting minigames in place of random greedy decisions were too costly.
Restricting actions: Sometimes we know that certain actions are always worse than others, for example, when there is only one active nondetermined minigame. We can forbid choosing these actions in UCT, which normally tries them too. This helps, yet there are two obstacles: it is again too costly, and perhaps disturbs the statistics of a node because the same node can be used for different game states with different excluded actions.
Here is my postmortem: reCurse's Codingame Summer Challenge 2024 Postmortem · GitHub
Thanks CG for the contest and the competitors for being great again!
#4, C++
Thanks to the entire UWr Team: @gaha, @surgutti, @Zylo, @DomiKo, and especially, of course, @MSz.
I am possitively surprised by the game idea. The level of originality was high (which is not easy given how many different games are already on CG). And having one action used in four different games seem hilarious.
On the other hand, the visualization was the worst ever (and Iâm pretty sure I had similar thoughts a few contests ago, so CG is âimprovingâ in that regard).
Totally useless:
player actions are not shown in a proper way (you need to look at diving - if it is not restarting).
no player messages.
it doesnât show track bars and player positions in hurdle, no info about remaining stun. (CG used the âon hoverâ feature years ago in-game visualizations - did they forget??)
no position/distance of player pointers in archery.
no traveled distance & stun in skating.
not even an option for a debug mode to pretend there may be some useful data there. No - itâs useless.
My approach and used techniques are overall pretty simple:
standard DUCT (one independent tree per player)
simulations one-generated-game-deep (except skating, which I do not generate at all - it is just computationally costly chaos - removing it lead to improvement)
solver for known games, which allows optimal moves for them
simple greedy policies for generated games. I tried multiple fancy options for skating (taking into account stunned opponents, etc.), but nothing was significantly better than some simple 3-rule policy. For archery it is just 1-turn greedy to be closest to the center.
policy moves return sets (and then I choose randomly), which works better than assuming there is only one best move, especially for hurdle/archery.
long term policies per player (which is choosing a game to try to optimize), which can deviate to short term policies if we are stunned. Games are chosen with uniform random - I wasted a lot of time trying some smarter choices here, but it wasnât working better.
use policy move selection instead of UCT for nodes with a small number of visits.
the evaluation function is based on medal points (with some basic assumptions on future games) and differences in scores between me and opponents.
OK, maybe itâs not THAT simple, but honestly, no extremely fancy things inside.
the engine doesnât simulate games that are useless. This include games which will not finish before turn 100, and games which should be generated second time, as others are still going during sim.
dynamic optimal move for hurdle (also for generated ones) with at most three array lookups. I didnât pre-generate all possible scenarios.
general rule: keep frequent parts as light as possible, precompute everything you can (but note the access cost to big structures).
Thanks to CG for organizing the challenge; the entire community for having good time together and see you at the next one.
(BTW: CG could you PLEASE make announcements faster - more than a few people really do plan tasks around your contests so info less than two weeks before is a sad joke.)
I like the concept, but I struggle a bit, I think. I need to practice more