https://www.codingame.com/training/medium/3n-tiling
Send your feedback or ask for help here!
Created by @CyberLemonade,validated by @R2B2,@damiengif and @JBM.
If you have any issues, feel free to ping them.
https://www.codingame.com/training/medium/3n-tiling
Send your feedback or ask for help here!
Created by @CyberLemonade,validated by @R2B2,@damiengif and @JBM.
If you have any issues, feel free to ping them.
I cannot pass 3xN intermediate test case, it fails on 3x12
My logic is:
dp[i] = (dp[i-1] + (i >= 3 ? dp[i-3] : 0) + (i >= 6 ? dp[i-6] * 2 : 0))%mod
it should return 154 but mine return 124, any idea?
You are missing some options that become available at 3x9 (think about whats possible in 2x9 - thats always possible in 3x9 too as you can just add a line of flat length 3 blocks on top of it).
@RoboStac thanks for the response, I managed to get some logic right. This is what I have now:
dpHeight1[0] = 1//height = 1
dpHeight2[0] = 1//height = 2
dpHeight3[0] = 1//height = 3
for (int width=1; width <= n; width++) {
//take out one 1x3
dpHeight3[width] = (dpHeight3[width-1])%mod
if width >= 2 {
dpHeight2[width] = (dpHeight2[width] + dpHeight2[width-2])%mod
}
if width >= 3 {
//put 1 time 3x1
dpHeight1[width] = (dpHeight1[width] + dpHeight1[width-3])%mod
//put 2 vertically stacked 3x1
dpHeight2[width] = (dpHeight2[width] + dpHeight2[width-3])%mod
//take out 3 vertically stacked times 3x1
dpHeight3[width] = (dpHeight3[width] + dpHeight3[width-3])%mod
//take out 1 time 2x2 and put it on top of 1 time 3x1
// or take out 1 time 3x1 and put it on top of 1 time 2x2
dpHeight3[width] = (dpHeight3[width] + 2 * (dpHeight2[width-2] * dpHeight1[width-3]))%mod
}
}
Looks like still not quite there, can you please advise what I’m still missing?
Failing on the same testcase:
beyond intermediate 3xn is failing, e.g. 3x12 should be 154 mine is 98.
Any help is really appreciated, have stuck on this for days 
Thanks
For N*3 Intermediate I have found a recurrence relationship, but it seems not right… with initialization f(0) = 0, f(1) = 1, f(2) = 1, f(3) = 2, g(0) = 0, h(0) = 0 I get the wrong results
I’m kinda lost from now, did I made an obvious mistake ?
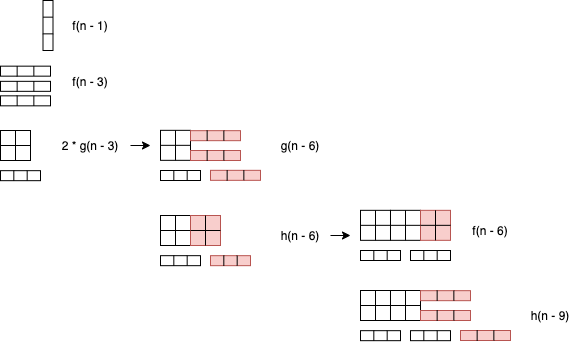
f(n) = f(n - 1) + f(n - 3) + 2 * g(n - 3)
g(n) = h(n - 3) + g(n - 3)
h(n) = f(n) + h(n - 3)
To illustrate how I end up with that :
Solutions now available @ CodeChef: [nope]
One point I’m struggling with is the huge sum of possibilities at width 3.
For example at length 9 we can do :

Which can be done in 4 ways (flip upside-down, and invert the middle square with the sticks)
Then at length 12 :

Which can be done in 6 ways (additional switches in the middle).
And so on, every 3 steps we get a new possibility with a coefficient of +2 compared to the previous one. (2 4 6 8 10 etc). Having put that into code it works, I get the right answers. But it slows down significantly for huge numbers because of how much back looping is involved.
So basically Im wondering if this is the right approach and I should find a way to optimize the process, or if I’m thinking about it the wrong way.
Edit: to clarify I get the following formula
L(i) = X + 2 * L(i - 6) + 4 * L(i - 9) + 6 * L(i - 12) + … (not spoiling the X  )
)
which means L(i) = X + Sum(2n * L(i - 3 * (n + 1))) for 1<= n <= i/3 - 1.
For huge numbers this is very cpu intensive and doesn’t go fast enough.
As much as I love this puzzle, I think that my biggest issue with it is that its in medium. There’s just so many things to put together to do this puzzle, I really think it could be in hard or every very hard.