Coding Games and Programming Challenges to Code Better
Send your feedback or ask for help here!
Created by @alexcercos,validated by @OEtzi007,@Nowan and @b0n5a1.
If you have any issues, feel free to ping them.
Coding Games and Programming Challenges to Code Better
Send your feedback or ask for help here!
Created by @alexcercos,validated by @OEtzi007,@Nowan and @b0n5a1.
If you have any issues, feel free to ping them.
It would have been better if the number of steps you give gives a proper interval between weights (for steps = 3 you have an interval of 0.5 but in your test cases you give steps = 10 for example which will give intervals of 1/9)
I don’t know bezier curves and don’t really wish to google for a basic problem. Please provide more details, especially the meaning of “Interpolate A and B to get one point AB” and what is the role of the wheight “t”
If you have two points X and Y and steps == n, you must calculate coordinates of n points A_0(x_0, y_0), A_1(x_1, y_1), …, A_(n-1)(x_(n-1), y_(n-1)) where X= A_0 and Y = A_(n-1) :
xi = t * x_0 + (1 - t) * x_(n-1) and y_i = t * y_0 + (1 - t) * y_(n-1) with t = i / (steps -1), i =0, 1,2, …, n-1
For example, if steps == 3, you get : A_0 = X, A_1 = midpoint(X, Y), A_2 = Y
The explanation of this problem is poor and makes the problem less “easy” simply due to poor explanation.
Yes, that really clears it up.
But if you know the Bernstein polynomials, the puzzle is really easy.
Yes i ask me the same thing
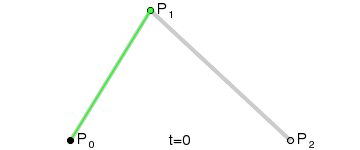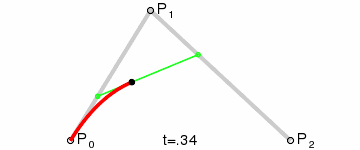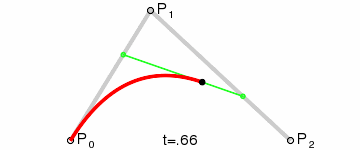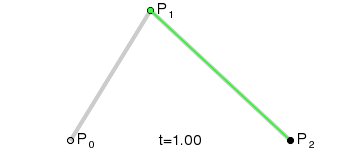
Thank you for this puzzle! I really like your explanation and the simplicity. I was looking for a puzzle to prepare for the moon landing that uses Bezier curves. I really appreciate you giving me an easy puzzle with this concept at the center.
Now for the more negative feedback.
It would be lovely to have tests for different levels of interpolation
I also like the idea of having interpolation step that can be divided by 10 easily so that debugging is simpler.
I’ve managed to get confused by the very short explanation. I thought A and B are start and finish, so I was interpolating the wrong thing. Maybe give them names of P0, P1, P2, P3 to reduce confusion.
The rounding of coordinates is somewhat confusing too. I tried storing points having integers as x and y, but I needed to round them when printing.