Coding Games and Programming Challenges to Code Better
Send your feedback or ask for help here!
Created by @java_coffee_cup,validated by @haiko256,@Malte42 and @presidentaz.
If you have any issues, feel free to ping them.
Coding Games and Programming Challenges to Code Better
Send your feedback or ask for help here!
Created by @java_coffee_cup,validated by @haiko256,@Malte42 and @presidentaz.
If you have any issues, feel free to ping them.
Great puzzle! I loved the combination of the geometry and the optimization. Very hard for me and oh, so satisfying when I finally finished!
Hello.
I am confused a bit - whether I should reorder cylinders (in box) or should I simply calculate the width strictly in given order of cylinders…
You have to reorder them to the minimum width.
I’m wondering if there is a O(N) solution without exploring all permutations…
I do not know a O(N) solution but I know some combinations can be skipped without a full test.
Standard Output Stream:
9.657
24.000
6696.314
1639.777
51.856
Found:1639.777
Expected:2163.508
3 542 93 150 135 380 10
My solution gave such order
3 542 93 150 135 380 10
It is best to prove the correctness by yourself.
If you cut out the circles in paper with radii in a correct ratio and arrange them on a line, you can confirm whether the total length can be a ratio of 1639 or should be much more.
Hi, I don’t understand how circles with radius of 3, 2, 2 and 1 can give a minimal width of 9.657.
I found 15.191
I think I’m misounderstood an information but I don’t know which.
Are you reading the statement correctly?
A line starts with integer m, for the number of cylinders, followed by m integers, for the radius of each cylinder.
I have no idea about how should I solve this one, so I asked bing AI, and the result was…
you can measure it using a ruler or another measuring tool. Is there anything else I can help with?
Time limit is very strict.
I had to replace all vectors with arrays and even precompute a table of sqrts to be able to pass. Unless my solution is of wrong complexity, I would have liked a problem with a less strict time limit.
Some combinations can be skipped, not needing a complete loop through. It may save about 1/3 or 1/4 of running time.
Without using this skipping strategy, my code in java can loop through all combinations within time limit.
Perhaps java nowadays is surpassing some other mainstream languages in efficiency to the extend that I am not aware of.
Hello
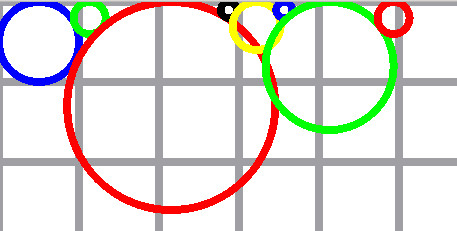
In the cylinders problem, for the first test, titled “Example”, the last serie of radii says to lead to a distance of 53.811.
The only way to get 53.811, it’s to place the radii like this : 5 2 13 1 3 1 8 2
But the fifth circle (radius 3) intersects the 3 and 7 circles. So this arrangement is not valid and prove the incorrectness of the algorithm. And the 7th circle intersects the third one.
You can cut out the circles in paper with radii in a correct ratio and arrange them on a line to see that.
Compare yours with mine.
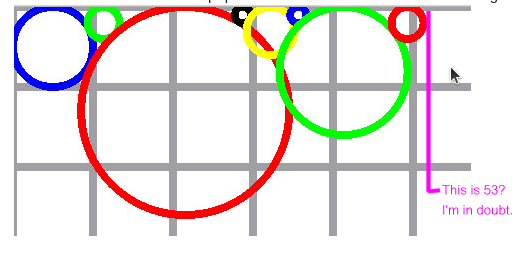
You’re right.
I’m in the error.
Hello,
What are the languages people have managed to pass the time limit with?
My Perl solution words locally and I cannot figure out more optimizations. Could the time limit depend on the language? That would prevent me from reimplementing this in a “fast” language like C to succeed this puzzle.
Regards,
There are successful solutions in python3, php, rust, typescript, java, c and c++.
Python and java are known to be some of the slow languages and yet they can pass.
Is a bad idea use a recursive function to calculate the right (and valid) position of the n+1 circle ?
A brief overview of my code (wich is too slow ![]() ) is: i have to decide at wich X-coordinate i have to position the (centre of) n+1. At first i stick to the n_th circle in a “provisory” status, then i check if, in that position, it would intersect other circles before the n_th (so starting from the n-1 and going back till the first). Then (recursively) starting from the “first occurence” of a in intersection i calculate the “new-provisory-position” and i re-calculate if there are STILL intersection with some of the circle in the back of the line. When there are no more intersection i accept the newest position as a final position for the n+1 circle. (still i’m not passin some test, in the example only the 3 380 135 150 542 93 10 comb i return the wrong number, in “caves to fill” i’m wrongly calculate 60 70 80 10 30 40 300 and in “hars” is this 1 my problem 914 398 108 36 688 846 231. Yes for every case i’m wrong in olny 1 line grrrr, and the last 1 , ofc, i fail for time out). Thank you very much for the help
) is: i have to decide at wich X-coordinate i have to position the (centre of) n+1. At first i stick to the n_th circle in a “provisory” status, then i check if, in that position, it would intersect other circles before the n_th (so starting from the n-1 and going back till the first). Then (recursively) starting from the “first occurence” of a in intersection i calculate the “new-provisory-position” and i re-calculate if there are STILL intersection with some of the circle in the back of the line. When there are no more intersection i accept the newest position as a final position for the n+1 circle. (still i’m not passin some test, in the example only the 3 380 135 150 542 93 10 comb i return the wrong number, in “caves to fill” i’m wrongly calculate 60 70 80 10 30 40 300 and in “hars” is this 1 my problem 914 398 108 36 688 846 231. Yes for every case i’m wrong in olny 1 line grrrr, and the last 1 , ofc, i fail for time out). Thank you very much for the help ![]() p.s. using python !
p.s. using python !
i stick to the n_th circle… i check if, in that position, it would intersect other circles before the n_th (so starting from the n-1 and going back till the first)
While we do not know what kinds of “intersection checkings” were done in your case, I assume this checking is a relatively expensive one, costly on CPU cycles and on memory usage. These two factors are the most common causes of TimeOut.
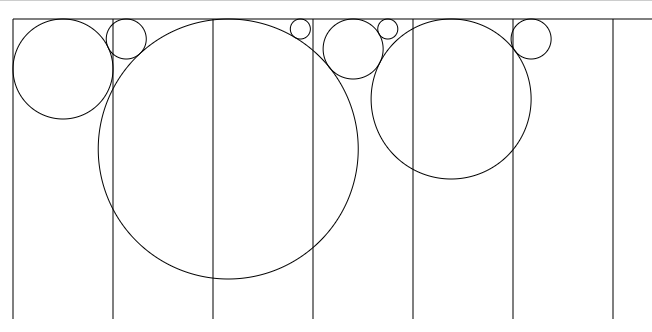
For illustration, I borrow the excellent diagram done by @FoxLee above. If you want to know is circle E intersecting with other circles, according to your algorithm you have to “check” it against circles A, B, C, D. Four times of costly checking.
Costly check E and A, is it really necessary? Based on their x-axis center and on their radii, I can immediately exclude A.
Algebra lovers may tend to solve two circle equations to find any intersection points. That is doable but really costly.
Recursion looks elegant but is too costly on memory. Try use iterative structures.