https://www.codingame.com/training/medium/detective-pikaptcha-ep3
Send your feedback or ask for help here!
Created by @java_coffee_cup,validated by @eulerscheZahl,@MadKnight and @pac-nam.
If you have any issues, feel free to ping them.
To align the description of the mobius to the viewer effect, the diagram in the puzzle is going to be updated.
What I didn’t catch during the contest is that you can jump over the top edge (or the bottom edge) to continue the path on the other side.
I aware that there are other players not noticing it too, so in the rewrite I stressed it two times in the statement.
There’s a drawing I proposed in the design phase.
1 Like
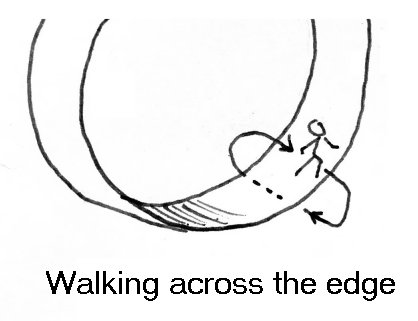
I don’t think this drawing matches what we are seeing in the puzzle.
cus it shows the same X axis while looping around Y axis.
Hmm…you are right. It was in early design not yet covering all properties. Now it should be modified like this:
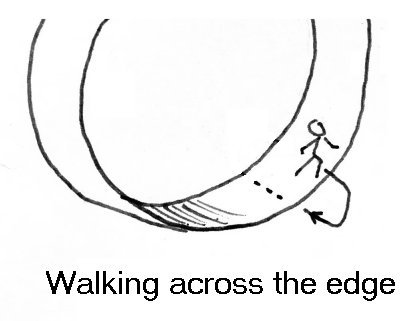
The drawing is correct if you assume that the grid has been mapped beforehand on a paper as instructed in the rules.
I would like to add a notice, as it took me some time to figure out why my solutions are not working(after reread the description properly 
).
The solution is not what the description asks.
Lets assume we have the front side of the strip with named corners:
A-----------------------B
|. . . . . . . . . . . . |
C-----------------------D
And the other side of the strip flipped over along the A-C axis vertically(and lets write its partner letter from the other side of the paper) :
E(B )------------------F(A )
| . . . . . . . . . . . .|
G(D )-----------------H(C )
If we twist this paper strip and make a Mobius strip from it, than we should get the below presented connection of neighbouring corners, “-” showing where the paper is taped together:
A-G … H-B
| . | … | . |
C-E … F-D
However in the testcases, the expected mapping for the neighbouring taped corners is something like this:
A-E … F-B
| . | … | . |
C-G … H-D
1 Like
I thought it should work like this.
Front side:
A-----------------------B
|. . . . . . . . . . . . |
C-----------------------D
Then flip the paper around a horizontal axis and get this:
E(C )------------------F(D )
| . . . . . . . . . . . .|
G(A )-----------------H(B )
When making the Mobuis thingy you would get these connections:
A-F … H-C
| . | … | . |
B-E … G-D
My solution doesn’t work… so I possibly did not understand the instructions correctly.
However, I wonder how it actually works. Your solution (turning the paper along the vertical axis) and my solution (turning the paper along the horizontal axis) does not return the expected connections.
Somehow I managed to get the first example right. But I am completely lost concerning the second example “circle”. I don’t quite understand how Detective Pikaptcha can get out of the middle area and to the two parts at the left and right side. Any hints?
Without modifying the initial grid, you can consider these connections:
6 Likes
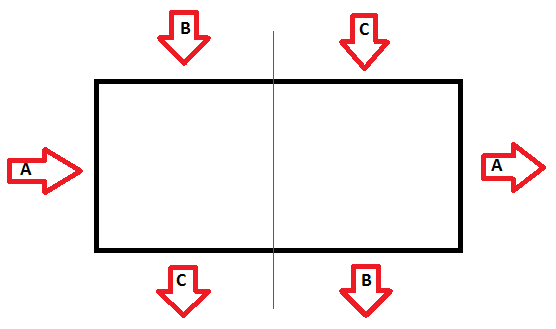
Thanks a lot Xa2017! I think I get it now. So you write the maze on a sheet of paper, fold it in half to get the strip with half of the maze on the front side and the other half on the backside and then create the Mobius “ring” out of this strip.
It might be just me but I find the instruction “Flip the paper over vertically” a little confusing. To me, it implies that the paper should be flipped around its Y axis, while in fact, it’s around its X axis.
4 Likes
The idea of doing a maze with a weird topology is cool but there are fundamental mistakes in this topology.
It really looks nothing like a moebius strip or any existent classical topology.
Edit 2: after solving the puzzle and reading the description more carefully, I understand why you describe it as a moebius strip. I was too focused on the topological definition, in topology we consider that surfaces don’t have “2 sides” so the moebius strip is like a weird non orientable little world where after a bit of travelling you can go back to a place you were before but with the opposite orientation as before.
It would make funny mazes too.
Yours is more a “real world” moebius strip that’s orientable and, as stated below, is topologically equivalent to a torus.
I made a sketch to recall the basic surfaces and the way you “glue” their edges:
You can see that the topology of this puzzle lies nowhere. I don’t know if it’s even possible to glue like that.
Edit: I was trying to glue the blue together and then had trouble vizualizing the other glueing but if you glue red first it’s easier, you just have to twist it a bit and then tou can glue blue and green.
So in the end it’s just …a Torus.
The Klein Bottle or Projective Plane would have been perfect for this puzzle tho.
3 Likes
The topology was a moebius strip in initial design stage but somehow a constrain of the structure was removed (edge boundary) by majority decision in final design so you can say it is an altered moebius or also very legally say it is nothing. Now I cannot easily change the statement. The discussion here is effectively the attachment and explanation to the statement.