I created some pic to visualize the n=12, k=5 & k=7 examples:
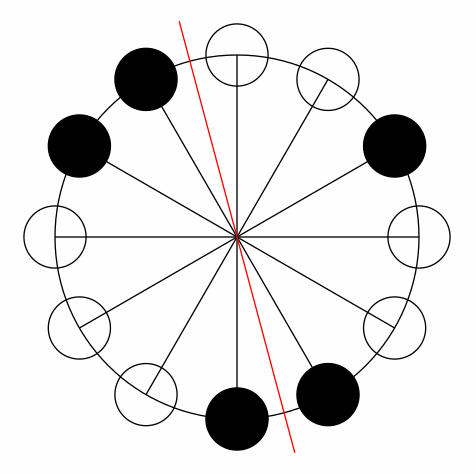
I understand how the masses can balance, but am having trouble quantifying
these instances where the gcd(N,k)==1
Can I assume all I have to do is find a sum of divisors or is it prime divisors that sum N?
I’ve been trying all kinds of variances that solve for some, but not for others. Any hints?
This is an intersting problem and I enjoyed spending time on it but I wish the statement would have been clearer about what this puzzle tries to achieve.
Basically there are two parts in this puzzle :
- the math problem
- the implementation of the solution
I believe that the author was more focused on the second part and assumed everyone would jump to the solution given in the video linked.
Except that it doesn’t work like that.
For people who enjoy solving math problems, jumping to the solution is actually the last thing you want to do.
As the statement is simple and nothing tells that the problem is actually pretty hard (I’ll come to that later), I tried to solve it by myself.
I could solve the case where N is even pretty fast.
Then when N is odd, I could demonstrate that when K is a multiple of a prime factor of N, it works.
And then remains the critical part: when K is a linear combination of prime factors of N.
Cause sometimes it doesn’t work at all (e.g. 8 = 3 + 5 doesn’t work for N = 15),
and sometimes it does (e.g. 8 = 3 + 5 does work for N = 45).
So after some struggling I found a “symetry” condition that was necessary for K to work, but was totally unable to prove if this condition was sufficient.
I spent time on it and ended up giving up the demonstration, submitting as if the condition was sufficient to see how far I was from the real answer and… completed 100% of testcases/validators.
Which is cool but is not satisfying from a math perspective, cause you want to know why it works.
So I did a bit of research and discovered that this result remained actually as a conjecture for a long time and was demonstrated quite recently (in 2010) in a research paper !
I got to admit that I was a bit upset about that, I mean how can you throw such a hard problem without any warning ?
So I don’t know, I don’t question the legitimacy of this puzzle, but there should definitively be some disclaimer about the difficulty of the math problem.
I propose to add something like this:
Note: If you want to solve this problem without external ressources,
be aware that the underlying math problem is challenging, the main
result has been demonstrated only in 2010.
This problem really requires sitting down, take a deep breath and put some effort to research a bit to solve. First, the Math. By looking at linked video, the math is straight forward:
For given N total holes, and K test tube, it can be balanced if and only if both K and N-K can be expressed as sum of prime number factors of N.
Now, the implementation part, 2 algorithms are needed. First, generate all prime number factors for given N. Second find if given K and N-K can be expressed in sum of those prime factors. First part should be easy, some research will give you answer straight away. For second part, the best hint is
use dynamic programming to figure out all K in one go. Here is a simple example to those who looking for help:
See if you have prime number factor of 2 and 3, suppose K is 16, which is valid because 2+2+2+2+2+3+3 = 16. DO NOT trying to track down as 16-3-3-2-2-2-2-2=0. This will give you time out. Instead, for factor 2, all its multiples 4, 6, 8, 10 … are valid. for 3, 6, 9, 12… are valid. Say when 13 is encountered, 13-3 =10 which is multiples of 2, so 13 is valid, now 16-3=13, because 13 is valid and we added 3 which is one of prime factor, so it is valid.