https://www.codingame.com/training/medium/ways-to-make-change
Send your feedback or ask for help here!
Created by @lhm,validated by @java_coffee_cup,@SinOfWrath and @codybumba.
If you have any issues, feel free to ping them.
Nice puzzle but there’s still an issue with validator 5.
The problem was raised 2 days ago by SinOfWrath but not fixed and the contribution got validated in the meanwhile.
Basically the problem is that validator 5 features an edgecase that does not appear in the testcases and even if it matches the constraints, it makes so little sense that people could spend a long time before thinking about it.
So what do you think ? Should we edit validator 5 to make it more similar to testcase 5 ?
Or add a testcase similar to validator 5 ?
Edit: the more I think about it, the more I want to just remove it cause really Vi = 0 does not make sense, it could lead to infinite number of combinations, for example if the set is {0, 1} you have 1 = 1 + 0 = 1 + 0 + 0 etc.
4 Likes
agree 
:}
Yeah, Vi = 0 does not make any sense, I think I avoided this validator issue only by chance.
Problem solved, Stilgart edited it.
It’s the other way around, you sum 1 coin 10 times.
Interesting challenge, but I’m stuck on last test case: solution not optimized.
Message to moderator : I’m not sure what I can write in this thread, so remove if innapropriate.
I’m using a tree to build the solutions, represented by the leaves.
Of course, with sum = 1000 and the smallest possible coins, the tree is quite huge.
There may be a more mathematical solution to optimize my algorithm. I already did it when the sum within the tree is higher than the requested amount. But so far, I’m clueless for this last test case…
Any clue ?
[edit] I tried using list instead of vector, which may be more optimized in this case, but I was unable to : error in algorithm when including list…
Say you want to find the number of combinations for an amount N.
If you already computed the number of combinations that gives all amounts from 0 to an number N - 1 and stored them in an array C, couldn’t you determine C[N] from C[0], C[1], …, C[N-1] ?
3 Likes
Thanks for the hint… Need to think more about it was definitely not the path I went first…
My dad and I have struggled with Test Case 6 for hours and hours, but we just can’t figure it out. We used recursion, and we don’t know how to make it efficient enough to solve Test Case 6. Could someone please give us a hint?
We also couldn’t understand pardouin’s earlier comment…
When the problem can be broken down into smaller and similar sub-problems, we can store the previous processed values into memory and take them out to reuse, to avoid duplicated calculation.
Do not open the hint if you do not wish to see it.
hint
When the world has only 1-dollar coin circulating,
ways to make changes for $1 to $10:
$=10 [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
When a 2-dollar coin is introduced, you have extra ways to make changes.
They are "EXTRA" ways. The original 1-dollar ways do not change.
Reuse previous calculated results.
$=2 [1, 2, 1, 1, 1, 1, 1, 1, 1, 1]
$=3 [1, 2, 2, 1, 1, 1, 1, 1, 1, 1]
$=4 [1, 2, 2, 3, 1, 1, 1, 1, 1, 1]
$=5 [1, 2, 2, 3, 3, 1, 1, 1, 1, 1]
$=6 [1, 2, 2, 3, 3, 4, 1, 1, 1, 1]
$=7 [1, 2, 2, 3, 3, 4, 4, 1, 1, 1]
$=8 [1, 2, 2, 3, 3, 4, 4, 5, 1, 1]
$=9 [1, 2, 2, 3, 3, 4, 4, 5, 5, 1]
$=10 [1, 2, 2, 3, 3, 4, 4, 5, 5, 6]
Focus on two lines from above. Try to understand the reasoning.
4 Likes
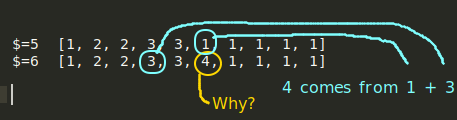
Thank you so much. We couldn’t have done it without you!
1 Like
hey, could not understand your hint.
Let’s take
$=2 [1, 2, 1, 1, 1, 1, 1, 1, 1, 1]
If we have a 2$ coin, it does not change the number of ways to do 1, hence there should be no extra way, for 2$ it is just one more way, so shouldn’t it be
$=2 [0, 1, 1, 1, 1, 1, 1, 1, 1, 1]
?
The array is the cumulative number of ways to do changes.
When you have both 1 and 2-dollar coins, the way to do change for $1 does not change, keeps at 1.
The way to do changes for $2 will be the original way + extra way for using the 2-dollar coin, so it is 2.
in that case, why the rest of the array is not all 2s then?
to make change for 3 we can do 31 or 22+1
The way to change with 2 kinds of coins and with amount of $3 is calculated in the $=3 line.
The $=2 line is valid for amount not exceeding $2.
Résumé
A first idea would be, if you call C[N] the number of ways to make N and your set of coins is {c1, c2, … } :
C[N] = C[N - c1] + C[N - c2] + …
but if you do that, some combinations will be counted several times, for example a combination “N = 1 + 2 + something” will be counted in C[N - 1] AND in C[N - 2].
Two ways to deal with it:
first option: let C[N][M] denote the number of ways to make N with a maximal coin of M, then you can go like this:
C[N][N] = C[N - c1][c1] + C[N - c2][c2] + …
second option: let C[N][M] denote the number of ways to make N with a minimal coin of M, then you can go like this:
C[N][0] = C[N - c1][c1] + C[N - c2][c2] + …
Both options work, and hint for a solution based on a recursive function. You’ll want to memoize the results to not recalculate the same things many times. It implies storing all values in a big cache, a 2dim array here (or let a builtin memoization feature do it for you).
You might have to set a higher recursion limit but it will work.
Now if you want to go further, if you’re familiar with those problems with recursive functions + memoization, you know that there is usually a way to get rid of the recursive function and build the cache yourself in an ascending way.
Here it’s particularly interesting cause when you fill the cache you realize that you don’t even need a 2dim array, you can only use a 1dim array and with the good chronology, modify the values in place and end up with the final state (the only one you actually need).
It’s a good way to save memory.
That’s how java_coffee_cup does it, he uses this chronology (step 1: maximal coin is c1, step 2: maximal coin is c2, etc).
Is it possible to get the solution for C++ ? I am stuck on this exercices for a long time and I can’t figure out how to solve it
I you still can’t solve it after all that’s been said, it might mean you’re not ready for this kind of puzzle yet.
Maybe try to solve easy puzzles first, there’s more than hundred of them:
Also, for this specific puzzle, this kind of problem is described here: https://cses.fi/book/book.pdf (from page 65), there’s the traditionnal change making problem and several other classics.
The codes are given in C++ so it’s perfect for you.
1 Like