I have implemented locally the “Maximum Likelihood Estimation” method, and applied it to two model cases.
**Case #1:**This case was given by Manwe in his posts.
[quote]Si on a deux joueurs avec des niveaux j1 et j2, J’ai choisi (et c’est très certainement perfectible) que:
la probabilité que j1 gagne seras:j1/(j1+j2)
la probabilité que j2 gagne seras:j2/(j1+j2)
Si on prends des exemples numériques avec j1=5 et j2=9, ça donne:
j1 gagne dans 5/14, et j2 gagne dans 9/14
Si on a j1=1, j2=9, alors j1 gagne 1 fois sur 10 etc
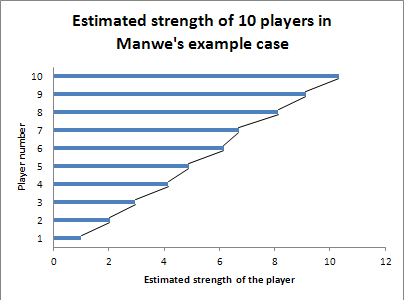
En faisant jouer 1000 matchs par IA, on obtient alors les courbes suivantes pour les scores de chaque joueur:[/quote]
My results with Maximum Likelihood Estimation are the following :
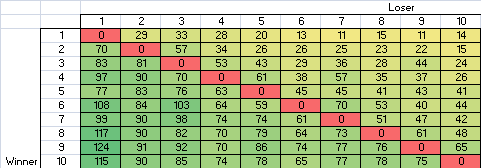
Case #2:
Case #2 is taken from the “Smash the code” TOP10 match history. It is a
sample of 800 matchs that I used to rank people relatively to each
other.
I don’t know how ties appear in the database, probably as a loss for one of the players…
My results with Maximum Likelihood Estimation are the following :
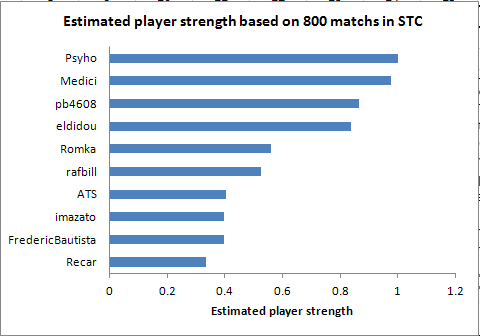
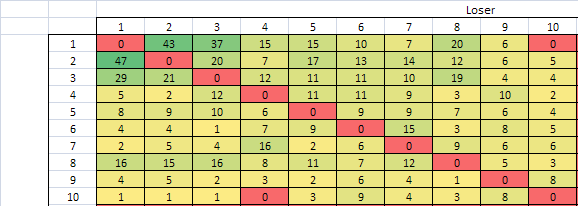
(I have to thank Magus for preparing the database)
My opinion at the moment is :
- Maximum Likelihood Estimation seems to be the theoretical best solution to fairly ranking AIs.
- Reading Manwe’s position, averaging the ranks upon stabilization doesn’t seem to be a bad solution, and might be easier to implement.
- In any case, the current opponent selection system should be modified so that the top2 players don’t play each other 50% of the time. I can provide simulations showing how much this skews the results…
- Also, the current system gives more matches the higher ranked you are. Once again, this can strongly skew the results and should be avoided in a fair ranking system. If adding new games for 2500 AIs isn’t doable, then it should be done for a subset (only 100 ? only 50 ?) but all the AIs in that subset should receive the same number of additional games.