It took me 2 hours to code a replay download/analyser. But it’s my job to do this kind of things. I don’t really want to publish it. It download all replays from the last battles page of someone. If everyone start to use it, Codingame will put a limit on it (like the submits with CGSpunk).
If you code in java, all you need is Apache Http Component and something to read the JSON (i prefer Jackson, but you can use Gson or standard java JSONObject).
Assume that I know how to download replays in Json 
, how do you approach the testing part?
Thx
Thanks 
I have read most of what LiHaoyi posted !
I’ll integrate some of your ideas in my next contests, like the Bundler and jmh tests.
A suggestion : keep in separated repositories common library code, and code specific to each CG contest. Those should be in private repositories actually … otherwise someone could just copy/paste your solution and achieve top100 in practice mode. I use gitlab for those.
Would you like to collaborate on a public repository of scala libraries for CG / AI stuff ? Maybe @csj would be interested too. Mine is a bit of a mess at the moment (https://github.com/tyrcho/scala-ai/), it would motivate me to organize it better There are for instance some generic implementations of minimax/alphabeta/MCTS.
24th Java referee based
It took me some time to write the post mortem, but here it is!
A great challenge as usual
I reached bronze league with a simple logic based on manhattan distances without any simulation.
I then started again from the referee code, and kept it for the whole competition. I did not had time to improve performances, but having the referee code was a huge gain in time.
Regarding performances, with this code and my evaluation function I was able to run maximum 600 simulations with the available 50 ms.
My bot proceeds first to an analysis of the situation to adjust some parameters (High level AI more details bellow). It then try to define what is the best order by doing a brute force search 3 turns in advance for each ship, considering the other ships are doing their best move if already defined, else considering they wait.
I start with the opponents ships and then compute this for my ships.
In the brute force search (A MaxNTree with only one player) I consider mining and firing only for the first turn in order to limit the branching factor (and cost to compute fire target) for the 2 next turns.
And that’s it !
A few details:
Depending on several conditions, I adapt a few parameters.
If there is more than two barrels left, I adjust the MAX_SHIP_HEALTH to 150 to trick the ships and make them believe they will have the entire rhum of the barrel. So that the ships do not wait near a barrel because they will have more rhum in 3 turns if they wait.
If there is no more barrel left, I adjust several parameters of the evaluation function in order to change my ships behavior. Main differences are for example the distance to the oponnent ships that I try to maximize if I am leading and I try to minimize on the contrary. More details in the evaluation function part bellow.
When I brainstormed on paper, I noticed that depending on the orientation and speed of your ship, the hexa distance and the minimum number of turns required to reach another cell is clearly different. Since I don’t see far away in the turns, making a difference between ships oriented differently can make the difference between a ship that turns or stays static because the barrel is behind it and in all cases in 3 turns it can’t be closer.
So during the first turn, I initialize 3 huge arrays of 50*50 integers where I brute force over the first 5 moves of a ships in the center position the minimum of moves required to reach a cell. I then complete the entire map by considering all the ships will be at speed 2 starting from the borders of the initialized cells.
Each map represent the “sailing distance” for each 0 1 2 speed with a fixed (0) orientation.
Example (cropped):
Speed 0, orientation 0:
Speed 1, orientation 0:
Speed 2, orientation 0:
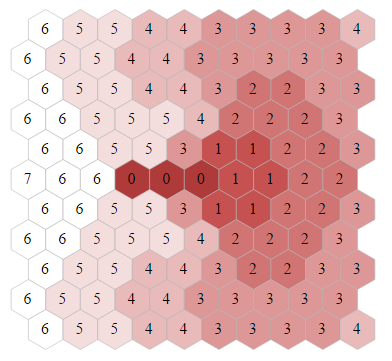
You noticed how the cell next to you when you have a speed of 2 is in fact already 5 turns away from you 
When I compute the sailing distance of 2 positions later on, I extract the ship speed and orientation, I compute the initial vector that it represent, I perform a rotation of this vector in order to put the ship in the 0 orientation, and I do a translation so that the ship is in the center cell. I then extract from the map the distance.
Using the Cube representation it’s quitte easy to do, and having these maps precomputed during the first turns it cost almost nothing more than computing hexa distances. Thanks codingame by the way for the article on the hexa grids, it was really helpfull!!
I first try to find barrels where an oponent ship is closer than me considering the sailing distance, and that I can fire on it before the opponent ship can reach it (still based on sailing distances and time to travel for the canon ball)
If there is none, I have an array of integers initialized to 0 for each ships and for each cell of the map. During the brute force search, I sum the health of the ship on each cell where it is present if it is greater or equal to it’s original health.
It builds a kind of presence probability for the next turns that take into account the fact that the ships will try to avoid damages, and favor capturing barrels.
I extract the cell with the maximum value and if I can fire on it in less than 2 or 3 turns I keep this as a possible target.
I also consider shooting to the mines, using the presence probability map in order to compute the sum of the neighbors divided by 3. I’ll shoot to the cell with the greatest score either a mine, either based on presence probabilities.
This fire order is then added to the list of possible moves and in my evaluation function I have a bonus when I fire in order to favor this move.
My evaluation function takes into account several parameters:
Depending on the situation, some parameters change and for example if there is no more barrels, either I try to flee from the opponent ships, either I try to get closer depending if I am leading or not.
Finished quite low at 808.
Here is my post mortem
video is no longer available.
Did you download it … ? 
plzzz say “yes” 
Hard to find this topic again with 2 R on CarRibbean… looked for “cotc” instead…
thanks, fixed
I believe Discourse search is quite bad too
I guess it’s long overdue for me to write my Post Mortem…
Here are in no particular order some thoughts that I implemented in my AI:
I am a firm believer that contests should be approached very progressively, by spending enough time to analyze the game with pen and paper. Writing code that is unused in the end is often a waste of time.
With that said, I believe that Coders of The Caribean is “2 games in 1”.
Question was: is it more important to fight well and kill the opponent in battles ? or think strategically and pick the last barrel ?
My answer at the time was: given the low frequency at which mines can be placed, the long flight time of cannonballs, the fog-of-war and the speed of ships, it would be difficult to kill an enemy ship.
Additionnally, the referee specified movement rules where a ship comes to a stop when it collides with any other ship. This is the main situation when a ship is at risk. Hence, I expected that any kill / evasion maneuver would appear in cooperation between several ships.
Hence, I’ll pick an algorithm where I can focus on evading & coordination between ships to pick the last barrel.
Surprised ? Yes, I did use genetic algorithms. Why so ? Here are a few reasons:
In my previous Post Mortems, I have described my “standard” approach with genetic algorithms : (1) Search what the opponent would do (2) Search what to do against this opponent prediction.
This approach isn’t optimal in COTC, because you might optimize against a specific predicted behavior 4 turns deep. The opponent prediction is highly imprecise and it should be considered so by the algorithm.
The basic algorithm can be modified in the following manner:
)This is similar to a depth 1 minimax algorithm, because I choose the path that **max**imizes my **min**imum score.
Following this principle, many options may be considered to represent the opponent behavior. I presented the simplest in this post-mortem, but believe me: I tried everything
Not much to say here. The only thing that I did not see in the thread was how I defined a “time-to-team-death” metric considering “perfect play” by my ships. This is basically :
rum_of_the biggest_ship + sum ( min(30, rum_other_ships) )
Other parts of the eval were already described by many people in the thread.
In hindsight, I would add the “special distance” described by @Manwe in his post-mortem : I really like the distance maps that were built
Hello Manwe, Thank you for sharing your experience. I really appreciate your way of thinking about distance. But there is one thing I don’t understand : How do you initialize your 3 huge maps during the 1st turn considering you can change the speed of the ship during the travel time?
Again thanks a lot
Make the map twice as big in each direction and place your ship in the center. Then all you have to do is to add an offset to your real ship and target location to move the ship to the center of your lookup map.
That way you only have initial speed and direction as parameters (I guess you can get rid of the direction too, but it’s fast enough without that optimization), so you have to run 18 breadth first searches on a map with 4 times the nodes of the actual map.
Ok, I understand that but i’m not sure how to run a BFS involving a modification a speed : For exemple if your initial speed is 0 and you want to go straight on to reach a goal 6 tiles in front of the center of your boat you will only need 3 turns : 1st you send “FASTER” and move foward one tile, then faster again and move foward 2 tiles and then a simple “WAIT” and you move foward 2 tiles and now the bow of your ship reach the goal tile. This is the simpliest exemple but it could be trickier with initial speed = 2 and a goal tile behind you.
You don’t try to reach a specific field, you find the distance to every field on the map.
From the initial position you have several options: WAIT, FASTER, SLOWER, RIGHT, LEFT.
This gives you up to 5 new positions that you can reach within 1 turn. For each of these apply the possible moves again. That might sound like a lot of possible states, but you will reach duplicate states (with speed 0 a RIGHT, LEFT is the same as LEFT, RIGHT or SLOWER,WAIT for example). The only important information for a state is your location, speed and direction, not the intermediate states you reached on the path, if you are interested in the distance only.
Oh ok thank you very much